|










- Number Bases
- General Floating-Point Representations
- ``The Most Important Fact'' About Floating-Point Number Systems
- Tables of Common Floating-Point Representations
- Sources of IEEE software and information
Number Bases
There are a variety of number bases. The most popular happens to correspond to the number of fingers your average human has on his hands. However, computers have a natural base of 2 corresponding to either on or off, high voltage or low. To represent a large number often requires a long string of 1's or 0's that gets a little cumbersome to write or work with on a sheet of paper. The Octal or Hexadecimal representation serves as a compromise between humans & computers. It allows humans to work with numbers that can be written in a compact fashion that translates directly to the computer's binary representation.Only rational numbers with denominators containing the same prime factors as the base have non-repeating fractional parts. In the above example repeating digits are represented with the strike-through font.
Base Example Decimal 10 10 .1 Binary 2 10102 .0 00112Octal 8 128 .0 63148Hexadecimal 16 A16 .1 916The following Fortran code fragment demonstrates one of the pitfalls of the floating point representation ... it's only an approximation and as such the programmer must be careful to realize that the actual computed result may not be the expected result.
parameter (zero = 0.0, one = 1.0, tenth = .1) a = tenth x = zero do 100 i = 1,10 x = x + tenth 100 continue error = x - oneThese results were produced on a Sun workstation using 32 bit IEEE representation.The expected results is zero. However, the computed results is small, but definitely not zero.
a = 0.10000000 x = 1.00000012 error = 1.1920929E-07 General Floating-Point Representations
The general floating point representation can be summarized as:x = +/- e - b x 0.d1d2...dp
where
+/- = sign bit (s) 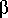
= base or radix dn = digit (0 dn <
-1)
(d1 0)
d = 0.d1d2...dp (mantissa) p = precision m = minimum exponent M = maximum exponent e - b = exponent - bias (m e - b
M)
where the following stipulation defines a normalized representation
And the special values -1
d < 1
where =
m-1 =
m x
.1
=
M(1 -
-p)
is the minimum positive value and
is the maximum positive value.
Example:
=2, p=3, m=-1, M=1
The only allowed non-negative values are:
.0,=.25, .3125, .375, .4375, .5, .625, .75, .875, 1., 1.25, 1.5,
=1.75

The assumption is made that for the basic numeric operations (+-*/) between any two floating point values the operation will yield a value that is a floating point value that's the nearest to the ``exact'' value.
Take for example the values .875 and 1.25 from above. The product of .875*1.25=1.09375; however, this value does not exist exactly within the floating point representation. The closest representable value is 1.0 which will (or should) be returned as the result of this operation.
If x is the result of the basic floating-point operations (+-*/) then the following assumptions will hold:
- If
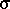
|x|
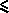
then x will be set to the nearest allowable floating-point representation.
- If |x| <
then the result is 0 which gives a ``silent and nondestructive underflow.''
- If |x| >
then calculation is terminated with a ``fatal overflow.''
``The Most Important Fact'' About Floating-Point Number Systems
The spacing between a floating-point number x and an adjacent floating-point number is at leastand at most x /
(unless x or the neighbor is 0). x
Therefore, the floating point representation corresponds to a discrete and finite set of points on the real number line which gets denser nearer the origin until it reaches some limit
. The relative spacing is proportional to
.
Table of Common Floating-Point Representations
All the representations shown are radix 2. The ones listed correspond to Cray parallel vector processors (PVPs), Digital Equipment Corporation (DEC) VMS VAX, and the last is the IEEE representation commonly found on workstations and for Linux boxes. The first table gives the single precision representation, and second table gives the double precision representation.
Fortran REAL and C float (Cray double) REAL CRAY VAX IEEE
length (bits) 64 32 32 sign bit (s) yes yes yes exponent (bits) 15 8 8 exponent bias (b) 3FFF 7F 7F fraction (bits) 48 23 23 hidden bit normalization no yes yes range low ( )
3.67x10-2466 2.93x10-39 1.175x10-38 2-8189 2-128 2-126 range high ( )
2.73x102465 1.701x1038 3.403x1038 28190 2127 2128 machine epsilon ( )
7.11x10-15 5.96x10-8 1.19x10-7 digits accuracy 14 7 7
Fortran DOUBLE PRECISION and C double (Cray long double) DOUBLE PRECISION CRAY VAX IEEE
length (bits) 128 64 64 sign bit (s) yes yes yes exponent (bits) 15 8 11 exponent bias (b) 3FFF 7F 3FF fraction (bits) 96 55 52 hidden bit normalization no yes yes range low ( )
3.67x10-2466 2.93x10-39 2.23x10-308 2-8189 2-128 2-11022 range high ( )
2.73x102465 1.701x1038 1.80x10308 28190 2127 21024 machine epsilon ( )
2.52x10-29 1.39x10-17 2.22x10-16 digits accuracy 29 17 16 The VAX & IEEE use ``hidden bit'' normalization. That is the first digit in the mantissa is assumed to be 1 and does not need to be ``stored''. The IEEE normalization is slightly different as noted below
The IEEE format also defines:
Cray (-1)s x 2e-b x .f VAX (-1)s x 2e-b x .1f IEEE (-1)s x 2e-b x 1.f
Inf : e = all one's and f = 0 NaN : e = all one's and f 0
Sources of IEEE software and information
- SoftFloat - freely available C code to implement IEC/IEEE floating point representation with software.
- Sun Microsystems' Numerical Computation Guide, which covers the IEEE Standard in detail.
Last Modified:










Brought to you by: R.K. Owen,Ph.D.
This page is http://owen.sj.ca.us/rkowen/howto/fltpt/index.html